Halveringstiden (T_1/2) är omvänt proportionell mot aktiviteten (A). Det betyder att den relativa osäkerheten i T_1/2 är densamma som den relativa osäkerheten i A.
Relativ osäkerhet i A:
(Delta A) / A = 5 Bq / 89 Bq ≈ 0.0562 (eller 5.62%)
Absolut osäkerhet i T_1/2:
Delta T_1/2 = T_1/2 * (Relativ osäkerhet i A)
Delta T_1/2 ≈ (1.526 * 10^11 år) * 0.0562
Delta T_1/2 ≈ 0.0857 * 10^11 år
Steg 4: Slutgiltigt svar
Vårt beräknade värde är T_1/2 ≈ 1.526 * 10^11 år med en osäkerhet på Delta T_1/2 ≈ 0.0857 * 10^11 år.
Vi avrundar svaret för att matcha precisionen i indata (två signifikanta siffror för A=89). Osäkerheten avrundas till en signifikant siffra (0.1) och värdet avrundas till motsvarande decimalplats (1.5).
Igår, 5 november: ”Remember, remember the fifth of November.” Dagen då Guy Fawkes och hans gäng katolska konspiratörer (1605) misslyckades med att spränga det protestantiska engelska parlamentet i luften.
Idag, 6 november: Gustaf Adolfs-dagen. Dagen då den protestantiske hjältekonungen Gustaf II Adolf (1632) dog på slagfältet vid Lützen under det pågående Trettioåriga kriget.
Två helt olika män, ett gemensamt tema: Båda är direkta produkter av 1500- och 1600-talens bittra och blodiga religionskrig i Europa.
En var en kung som ledde arméer för den protestantiska saken, den andre en extremist som försökte använda terrorism för den katolska. Det sätter perspektiv på hur djupt splittrad och våldsam kontinenten var.
Så, oavsett om ni firar med fyrverkerier (som britterna) eller en bakelse (som vi), är det två dagar som påminner om en tid då religion och politik var en… minst sagt explosiv blandning.
Här är en sammanfattning av konflikten som ger den nödvändiga bakgrunden.
📜 Sammanfattning: Det Engelska Inbördeskriget (1642–1651)
Det engelska inbördeskriget var inte ett enda krig, utan en serie brutala konflikter som splittrade nationen. Kärnfrågan var: Vem skulle styra landet – kungen eller parlamentet?
🤼 Huvudkonflikten: Kung vs. Parlament
På 1600-talet styrdes England av kung Karl I (Charles I). Han var en fast anhängare av ”det kungliga enväldet” – idén att en kungs makt kom direkt från Gud och att han inte behövde svara inför någon, inte ens parlamentet.
Parlamentet, å andra sidan, bestod av adelsmän och folkvalda (om än av en mycket begränsad del av befolkningen). De ansåg att kungen inte kunde styra utan deras medgivande, särskilt när det gällde att införa nya skatter och stifta lagar.
Konflikten var också djupt rotad i religion. Kungen gynnade en mer katolsk-liknande, ritualistisk form av protestantism (högkyrklig anglikanism). Många i parlamentet var puritaner – en striktare, mer radikal protestantisk grupp som ville ”rena” kyrkan från allt katolskt inflytande.
Konflikten eskalerade tills kungen försökte arrestera fem medlemmar av parlamentet 1642. Det misslyckades, och båda sidor insåg att krig var oundvikligt.
⚔️ Sidorna i kriget
Kungasidan (Royalists / ”Cavaliers”)
Ledare: Kung Karl I.
Stöd: Främst från den gamla adeln, prästerskapet och de mer lantliga, feodala delarna av norra och västra England.
Mål: Bevara kungens enväldiga makt och den traditionella kyrkans hierarki.
Parlamentssidan (Parliamentarians / ”Roundheads”)
Ledare: Parlamentet, men militärt blev Oliver Cromwell den avgörande figuren.
Stöd: Främst från köpmän, städer (särskilt London) och de mer puritanskt influerade delarna av södra och östra England.
Mål: Begränsa kungens makt och reformera kyrkan.
🌟 Cromwells Uppgång och Seger
Till en början gick det dåligt för parlamentet. Deras arméer var oorganiserade. Det var här Oliver Cromwell, en puritansk godsägare och parlamentsledamot, steg fram.
Cromwell var en militärstrateg av geni. Han skapade ”New Model Army” (Nya Modellarmén).
Till skillnad från andra arméer baserades befordran i Nya Modellarmén inte på adlig börd, utan på merit och skicklighet.
Det var en professionell, disciplinerad och djupt religiös (puritansk) armé som trodde att de utkämpade Guds krig.
Cromwells armé krossade kungens styrkor, framför allt i de avgörande slagen vid Marston Moor (1644) och Naseby (1645). Kung Karl I kapitulerade till slut 1646.
👑 Kungens Avrättning och Republikens Födelse
Detta var inte slutet. Karl I var hal och försökte ständigt förhandla och spela ut sina fiender mot varandra. Han startade till och med ett ”andra inbördeskrig” från sin fångenskap.
Armén och de radikala i parlamentet, ledda av Cromwell, tröttnade. De såg Karl I som en ”blodbesudlad tyrann” som aldrig skulle sluta skapa krig.
I en handling som chockade hela Europa ställdes kungen inför rätta för högförräderi mot sitt eget folk. Han dömdes till döden och avrättades genom halshuggning den 30 januari 1649. Oliver Cromwell var en av dem som skrev under dödsdomen.
Monarkin och överhuset avskaffades. England förklarades vara en republik, kallad ”Samväldet” (The Commonwealth).
🏛️ Cromwells Styret (Interregnum)
Efter kungens död inleddes en period utan kungar (1649-1660), känd som ”Interregnum”.
Cromwell blev snabbt den dominerande makthavaren. Efter att ha krossat uppror på Irland (med ökänd brutalitet) och i Skottland, upplöste han till slut det ineffektiva parlamentet med våld.
År 1653 tog han titeln ”Lord Protector” (Lordprotektor) och styrde i praktiken som en militärdiktator fram till sin död 1658. Han var djupt religiös, men också djupt kontroversiell. Vissa såg honom som en frihetshjälte, andra som en tyrannisk kungamördare.
🔙 Restaurationen (Monarkins Återkomst)
När Cromwell dog 1658 tog hans son Richard över, men han var en svag ledare. Systemet kollapsade snabbt. Folket var trötta på militärstyre och puritansk stränghet.
År 1660 bjöd parlamentet tillbaka den avrättade kungens son, Karl II (Charles II), från hans exil. Monarkin återställdes. Detta kallas Restaurationen.
⛓️ Kopplingen till Cromwells Huvud
Detta är bakgrunden till den makabra historien om Cromwells huvud. När Karl II återvände till makten var hämndlystnaden mot dem som dödat hans far enorm.
De som fortfarande levde och hade skrivit under Karl I:s dödsdom (de så kallade ”kungamördarna”) jagades, torterades och avrättades.
Men den främste kungamördaren, Oliver Cromwell, var redan död och begraven med statsbegravningspompa i Westminster Abbey. För de hämndlystna rojalisterna räckte inte detta…
Vill du att jag fortsätter och berättar den bisarra historien om vad som hände med Cromwells kropp och huvud efter Restaurationen?
Andraordningens differentialekvationer är ett avancerat ämne i gymnasiet, men det behandlas oftast i den sista matematikkursen (t.ex. Matte 5) och då i en förenklad form.
Här är en sammanfattning som fokuserar på de typer som normalt tas upp på gymnasienivå:
En andraordningens differentialekvation är en ekvation som innehåller den andra derivatan (dx2d2y eller y′′) av den obekanta funktionen y.
I. Den Homogena Ekvationen
Den vanligaste typen på gymnasiet är den linjära, homogena, andraordningens differentialekvationen med konstanta koefficienter.
Generell form:
ay′′+by′+cy=0
där a, b och c är konstanter (a=0).
Lösningsmetod: Karakteristisk Ekvation
För att lösa denna typ av ekvation ersätter man derivatorna med potenser av en variabel r, vilket ger den karakteristiska ekvationen (en andragradsekvation):
ar2+br+c=0
Lösningarna till andragradsekvationen, r1 och r2, bestämmer differentialekvationens allmänna lösning, y.
Tre fall för lösningen (y′′=f(y′,y)):
FallKarakteristisk ekvation (ar2+br+c=0)Rötter (r1,r2)Allmän lösning, y1.Två olika reella rötterr1 och r2 (r1=r2)y=C1er1x+C2er2x2.En reell dubbelrotr1=r2=ry=C1erx+C2xerx3.Komplexa rötterr1=α+iβ och r2=α−iβy=eαx(C1cos(βx)+C2sin(βx))
Där C1 och C2 är godtyckliga konstanter som bestäms av begynnelsevillkor (t.ex. värdet på y och y′ vid x=0).
II. Förenklade Typer (Reducering av ordning)
Vissa andraordningens differentialekvationer kan lösas genom att först betrakta dem som förstaordningens ekvationer.
1. Saknar y (y′′=f(x,y′))
Om ekvationen inte innehåller y (den obekanta funktionen), kan man substituera:
Låt z=y′
Då blir y′′=z′
Ekvationen transformeras då till en förstaordningens ekvation i z:
z′=f(x,z)
Lös först för z(x), och integrera sedan för att få y: y=∫z(x)dx.
2. Saknar y′ (y′′=f(x,y))
Om ekvationen saknar y′ (den första derivatan), är den ofta enklare att integrera direkt:
y′′=f(x)
Integrera två gånger:
y′=∫f(x)dx+C1
y=∬f(x)dx2+C1x+C2
Tillämpningar (Typiskt för Gymnasiet)
Andraordningens differentialekvationer används ofta för att beskriva svängningsrörelser (som pendlar eller fjädrar) inom fysiken.
Olbers paradox är en klassisk astronomisk gåta som frågar: Varför är natthimlen mörk?
Paradoxen uppmärksammades på 1800-talet av den tyske astronomen Heinrich Wilhelm Olbers, men den har diskuterats av tänkare ända sedan 1500-talet (bl.a. Kepler och Halley).
1. Själva paradoxen (Argumentet)
Paradoxen bygger på antagandet att universum är:
Oändligt stort
Oändligt gammalt
Fyllt med stjärnor som är ungefär jämnt fördelade (homogent).
Om dessa antaganden var sanna, borde natthimlen vara lika ljus som ytan på solen i varje punkt.
Resonemanget:
Betrakta en serie koncentriska sfäriska skal runt jorden.
Ljusstyrkan från varje enskild stjärna minskar med kvadraten på avståndet (1/r2).
Men antalet stjärnor i varje skal ökar med kvadraten på avståndet, eftersom skalets yta ökar (r2).
Därför tar den ökade mängden stjärnor ut den minskade ljusstyrkan.
Slutsats: Den totala mängden ljus som når oss från varje skal är densamma, oavsett hur långt bort det är. Om det finns ett oändligt antal sådana skal i ett oändligt universum, skulle varje synlinje oundvikligen sluta på ytan av en stjärna, och himlen skulle vara bländande ljus.
2. Lösningen
Paradoxen bevisar att minst ett av de ursprungliga antagandena om universum måste vara fel. De huvudsakliga, moderna lösningarna bygger på två centrala fakta om vårt universum (som vi känner till det sedan Big Bang-teorin):
A. Universum har en ändlig ålder (Viktigaste lösningen)
Universum är bara ungefär 13,8 miljarder år gammalt.
Ljusets hastighet är begränsad, vilket innebär att ljuset från de mest avlägsna stjärnorna helt enkelt inte har haft tid att nå oss än.
Det finns en ”kosmisk horisont” – det observerbara universum – bortom vilken vi inte kan se. Himlen är mörk i de riktningar som ligger bortom denna horisont.
B. Universum expanderar (Bidragande lösning)
Universum expanderar (som beskrivs av Hubbles lag), vilket orsakar rödförskjutning av ljuset från avlägsna stjärnor och galaxer.
Ju längre bort ett ljusobjekt är, desto snabbare rör det sig bort från oss, och desto mer sträcks dess ljusvåglängder ut (rödförskjuts).
Rödförskjutningen flyttar ljuset från synligt ljus till infrarött och mikrovågigt ljus, vilket gör att det framstår som mycket svagare eller osynligt för det mänskliga ögat.
3. Falska lösningar
Olbers själv föreslog att kosmiskt stoft absorberar ljuset. Denna idé är dock felaktig, eftersom stoftet som absorberar stjärnljuset så småningom skulle värmas upp och självt börja lysa (stråla ut energin igen), vilket skulle bibehålla himlens totala ljusstyrka.
Nedan följer en sammanfattning av Konstantinopels fall den 29 maj 1453, inklusive några av de mest fängslande historiska detaljerna kring belägringen. Denna händelse markerar ofta slutet på medeltiden och början på den tidigmoderna eran. Huvudsaklig källa är kejsar Konstantins sekreterare Georg Sphranzes som var med under slutstriden och överlevde. Men hans hustru och barn hamnade i ‘Mehmet 2 :s harem och hans son avrättades. Själv blev han friköpt och slog sig ner på ön Korfu och gick i kloster där under namnet Gregorius. Han dog 1478. Hans verk heter ’Chronica minus’.
Sammanfattning av Konstantinopels fall 1453
Konstantinopels fall var kulmen på en 53 dagar lång belägring, ledd av den blott 21-årige osmanske sultanen Mehmed II (”Erövraren”). Staden, huvudstad i det krympande Bysantinska riket (Östrom), hade stått emot belägringar i över tusen år tack vare sina legendariska Theodosianska murar – ett system av dubbla försvarsverk och en torr vallgrav.
1. Slaget om de stora kanonerna
Den mest avgörande faktorn i belägringen var artilleriet, särskilt den gigantiska kanonen känd som ”Basiliskan”.
Det ungerska geniet: Kanonen ritades av en ungersk ingenjör vid namn Urban, som först erbjöd sina tjänster till den bysantinske kejsaren Konstantin XI Palaiologos. Kejsaren hade dock inte råd att betala hans höga pris, varpå Urban gick över till Sultan Mehmed II.
En koloss av brons: Basiliskan var så enorm att den krävde 90 oxar och hundratals man för att transporteras till belägringsplatsen. Den kunde avfyra massiva stenkulor på upp till 500 kg som slog sönder de till synes ogenomträngliga murarna. Dock var den så långsam och krävde så mycket avkylning att den bara kunde avfyra 3–7 skott per dag. Ändå krossade Basiliskan successivt de yttre murarna, även om den själv havererade efter cirka sex veckors bombardemang.
2. Sjöstrider och det ”gående skeppet”
Staden skyddades i norr av Gyllene hornet, en vik som spärrades av med en massiv järnkedja för att hindra fientliga skepp.
Mehmeds genidrag: När den osmanska flottan inte kunde bryta igenom kedjan, beordrade sultanen en häpnadsväckande manöver. Under en enda natt (den 21–22 april) byggde hans soldater en träramp täckt med fett och stockar, och drog 70 osmanska fartyg över land (Galata-kullen) in i Gyllene hornet, bakom den bysantinska kedjan. Detta överraskningsmoment demoraliserade försvararna och tvingade dem att omfördela trupper från landmurarna.
3. Kejsarens sista strid
Kejsar Konstantin XI Palaiologos ledde personligen det underlägsna försvaret, som endast bestod av cirka 7 000 soldater (jämfört med Osmanska rikets uppskattningsvis 60 000–80 000 man).
Det sista talet: Kejsaren höll ett gripande sista tal till sina soldater, i vetskap om att slutet var nära. När osmanerna väl bröt igenom natten till den 29 maj, kastade kejsaren av sig sina kejserliga insignier och ledde en sista motattack vid den utsatta muren, där han stupade tillsammans med sina män. Hans exakta dödsplats och öde är okänt, vilket har gett upphov till legenden om Marmorkejsaren – att han inte dog utan förvandlades till marmor och sover under staden, redo att återvända för att återta den.
4. Hagia Sofias skändning och plundringen
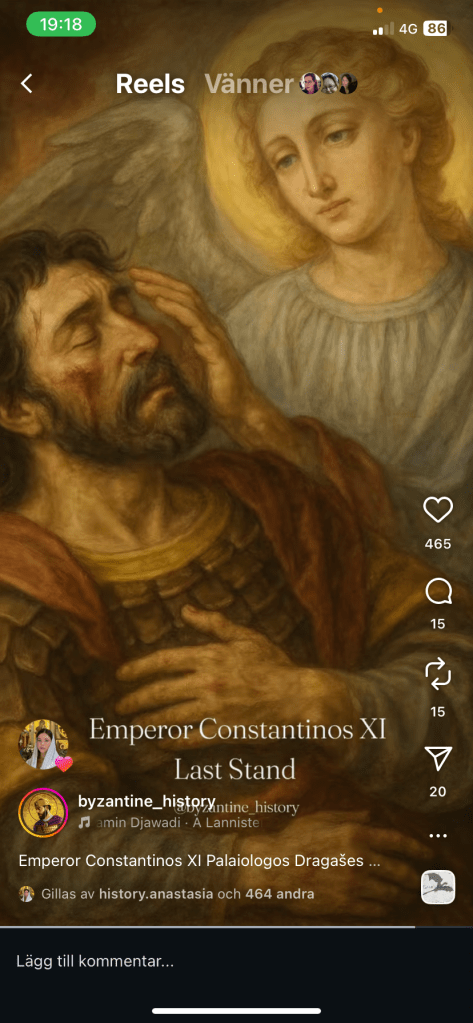
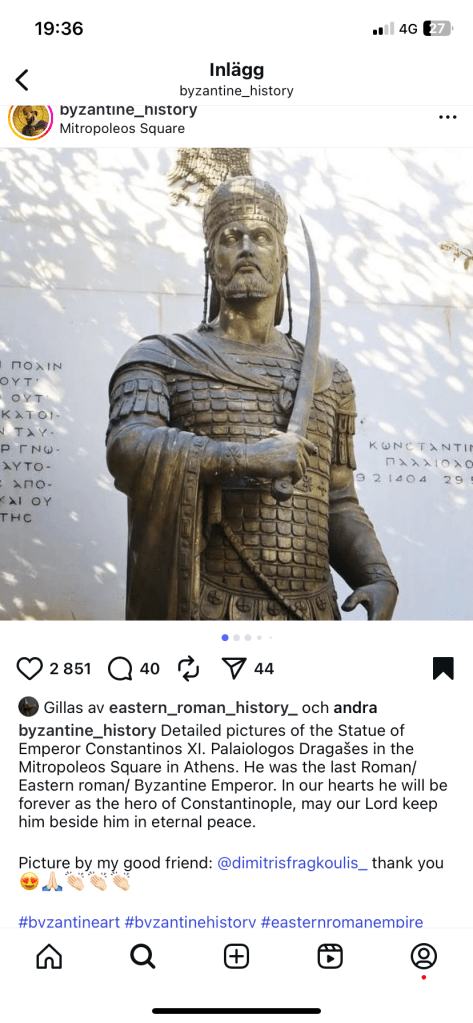
Efter att janitsjarerna (sultanens elitstyrkor) brutit igenom muren vid porten Kerkoporta, strömmade de osmanska trupperna in.
Asyl i Hagia Sofia: Tusentals civila hade sökt skydd i den storslagna kyrkan Hagia Sofia, i tron att dess helighet skulle skydda dem. De osmanska soldaterna bröt sig in, varpå människor våldtogs, dödades och förslavades. Ett ögonvittne till detta är kejsarens sekreterare George Franzes som sökt skydd i Kyrka med sin familj. Hans döttrar fördes till sultanens harem.
Mehmed II:s intåg: Efter tre dagars plundring – den sedvanliga ”segerrätten” – red Mehmed II in i staden. Han red direkt till Hagia Sofia, där han beundrade dess storhet, men beordrade omedelbart att den skulle omvandlas till en moské (vilket den var i nästan 500 år tills den blev ett museum 1934, och åter moské 2020).
Tiden tog slut: En intressant, och för grekerna symbolisk, detalj är att de gamla portarna till Hagia Sofia sägs ha stängts hastigt när den sista mässan hölls inuti. Än idag betraktar många greker tisdagen (dagen då staden föll) som veckans otursdag. Minnet av det bysantinska rikets sista strid och kejsar Konstantins heroiska död vid Romanosporten kom att för framtiden bestämma grekernas livssyn. När deras nationella stad återuppstod på 1820-talet betraktade de alltjämt Konstantinopel som sin ännu inte befriade huvudstad.
5. Konsekvenser för Europa och Renässansen
Konstantinopels fall ledde till dramatiska skiften:
Slutet på en era: Det Bysantinska riket, arvtagaren till Romarriket, upphörde att existera. Konstantinopel blev den nya huvudstaden i det Osmanska riket under namnet Istanbul.
Flykten västerut: Många bysantinska lärda flydde västerut och tog med sig ovärderliga grekiska och romerska manuskript. Denna flykt av kunskap bidrog starkt till att ge energi åt renässansen i Italien och resten av Västeuropa.
Stängda handelsvägar: Osmanska rikets kontroll över de centrala handelsvägarna mellan Europa och Asien tvingade europeiska makter att söka nya vägar till Fjärran Östern, vilket blev en katalysator för Upptäcktsresornas tid.
Innebar det inte att osmanerna obehindrat kunde tränga fram till wien?
Det är en utmärkt och helt relevant fråga! Ja, Konstantinopels fall 1453 innebar i princip att den sista stora barriären mot osmansk expansion i sydöstra Europa hade fallit, vilket gjorde vägen mot Wien betydligt öppnare.
Här är en sammanfattning av kopplingen och varför det dröjde ytterligare cirka 160 år innan den verkliga ”attacken” mot Wien kom:
Från Konstantinopel till Wiens portar
1. Eliminering av Bysans
Bysans hade länge fungerat som en buffertzon mot östliga invasioner. Genom att erövra Konstantinopel 1453 fick det Osmanska riket:
En permanent bas och en ny, strategiskt belägen huvudstad i Europa.
Total kontroll över Bosporen och Dardanellerna, vilket möjliggjorde obehindrad passage av trupper och materiel mellan Asien och Europa.
En massiv psykologisk seger som stärkte sultanens legitimitet och demoraliserade de kristna makterna i väst.
2. Den omedelbara expansionen i Europa
Efter 1453 kunde osmanerna ägna sin fulla militära styrka åt att konsolidera och expandera sina europeiska territorier. Deras expansionsriktning blev omedelbart inriktad mot Centraleuropa:
Balkan föll: Serbien, Bosnien, Albanien och Grekland (Morea) föll under osmansk kontroll under de följande decennierna.
Ungern hotades: Den stora konfrontationen stod mot Kungariket Ungern, som då fungerade som Europas viktigaste försvarslinje mot osmanerna.
3. Slaget vid Mohács och vägen till Wien (1529)
Den direkta vägen till Wien öppnades i praktiken efter slaget vid Mohács 1526.
I detta slag krossade den osmanske sultanen Süleyman I ”den store” den ungerska armén och dödade deras kung, Ludvig II. Ungern splittrades därefter, och en stor del av landet blev osmanskt.
Detta eliminerade den sista stora militära bufferten mellan det Osmanska riket och det Habsburgska riket (som styrde över Österrike).
Det var först tre år senare, 1529, som den osmanska armén trängde obehindrat fram till Wien för första gången, och inledde den första belägringen av staden.
Varför dröjde det 160 år till det stora slaget?
Även om vägen var öppen, var det inte en omedelbar marsch till Wien:
Logistik: Att flytta och försörja en jättearmé med artilleri från Konstantinopel ända till Wien var en kolossal logistisk utmaning som krävde långa förberedelser.
Mindre stater: Osmanerna var tvungna att erövra och säkra ett antal mindre stater och fästningar på Balkan och i Ungern för att säkra sina försörjningslinjer.
Habsburgs motstånd: Habsburgarna var en formidabel motståndare som kontinuerligt stred mot osmanerna i Ungern, vilket fördröjde det slutliga anfallet mot Wien.
Slutligen kan man säga att Konstantinopels fall satte igång den kedjereaktion som ledde till Wien. Det var det strategiska startskottet som möjliggjorde erövringarna på Balkan och Ungern, vilka i sin tur ledde till att osmanerna kunde hota Wien 1529 och igen 1683.
Det dröjde väl ända till 1800-talet innan osmanerna rensats ut från östeuropa och Balkan och tryckts tillbaka till Konstantinopel igen?
Det är helt rätt att det tog lång tid, ända in på 1900-talet, innan det Osmanska riket var helt utdrivet från Balkan och Östeuropa. Processen var långsam och plågsam, och den osmanska närvaron krympte i olika steg.
Här är en sammanfattning av hur tillbakapressningen till det som blev Turkiet gick till:
Osmanernas tillbakadragande från Europa
1. Vändpunkten: Wien 1683
Den första stora vändpunkten kom med Slaget vid Wien 1683.
Osmanerna, ledda av storvesiren Kara Mustafa Pasha, belägrade Wien för andra gången, men slogs tillbaka av en kristen koalition, ledd av den polske kungen Johan III Sobieski.
Detta var inte bara ett nederlag, utan det bröt den osmanska myten om oövervinnelighet. Det följdes av Stora turkiska kriget (1683–1699), där Habsburgarna och deras allierade erövrade stora delar av Ungern.
Karlovyč-freden 1699 tvingade osmanerna att avträda nästan hela Ungern till Österrike – ett enormt steg bakåt.
Prins Eugen av Savojen, österrikisk överste under stora turkiska kriget.
2. Nationella uppror och stormaktsrivalitet (1800-talet)
Det var under 1800-talet som utdrivningen tog riktig fart, drivet av två faktorer:
A. Uppvaknande nationalism
De kristna folken på Balkan, inspirerade av upplysningen och revolutionerna i Västeuropa, började kämpa för självständighet.
Greklands självständighet (1821–1829): Detta var ett tidigt och viktigt steg. Med stöd från Storbritannien, Frankrike och Ryssland tvingades osmanerna att erkänna ett självständigt Grekland.
Serbien, Rumänien och Bulgarien: Dessa regioner fick gradvis autonomi och sedan full självständighet efter krig mot Ryssland och Osmanska riket.
B. Rysslands expansion
Ryssland såg sig som beskyddare av alla slaviska och ortodoxa folk och förde upprepade krig mot det Osmanska riket. Ryssen pressade konstant söderut för att få tillgång till Medelhavet via Bosporen och Dardanellerna.
Rysk-turkiska kriget 1877–1878 ledde till att Rumänien, Serbien och Montenegro blev helt oberoende och att Bulgarien blev ett autonomt furstendöme (och senare helt självständigt).
3. Slutsteget: Balkankrigen (1912–1913)
Det definitiva slutet för den osmanska makten på det europeiska fastlandet kom i början av 1900-talet.
Balkankrigen (1912–1913) var de sista spiken i kistan. De nyetablerade kristna staterna (Grekland, Serbien, Bulgarien och Montenegro) allierade sig och drev ut de osmanska trupperna från nästan alla deras återstående europeiska territorier.
Efter Balkankrigen reducerades det Osmanska riket på den europeiska sidan (Thrakien) i praktiken till enbart staden Konstantinopel och dess omedelbara omgivning.
Sammanfattning
Man kan alltså säga att:
1699 markerar när Ungern förlorades.
1800-talet markerar när de första balkanstaterna fick självständighet.
1913 markerar när nästan hela Östeuropa och Balkan var rensat från osmansk kontroll, och riket var tillbakapressat till just det område där Istanbul (Konstantinopel) ligger.
Det Osmanska riket gick slutligen under i och med första världskriget, vilket ledde till etableringen av den moderna staten Turkiet 1922–1923.
How to draw Exceldiagrams
Miniräknare/calculator
Kristians Kunskapsbank 
